详解贝叶斯(一):贝叶斯概率
详解贝叶斯(一):贝叶斯概率
什么是贝叶斯概率
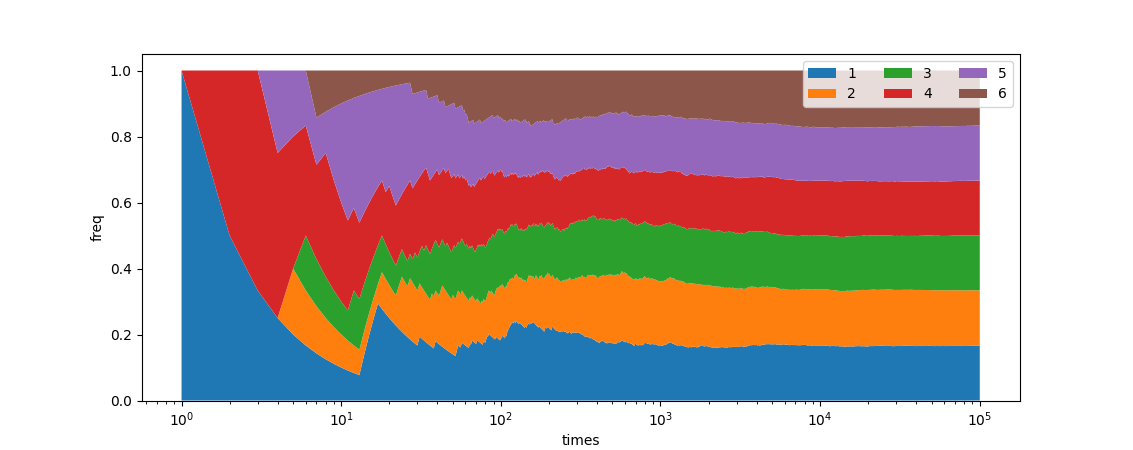
要解释什么是贝叶斯概率,不如先回顾一下经典的概率,中学课本里我们把概率定义为事件发生的可能性,认为概率是一个确定的值, 但是这个取值我们不知道。那这个值如何求得呢?可以通过统计事情的频率获得概率的近似。比如不断的抛一枚均匀的骰子🎲,随着次数的增加,统计的各点数出现的频率不断的趋近于一个定值,这个定值就是某个点数出现的概率。写段脚本模拟投10万次骰子,把各点数频率变化画出来就能发现均趋于稳定在\frac{1}{6},就是各点数的概率。当结果是一个不确定但可重复的过程的结果时,概率总是可以通过简单地观察多次过程的重复并计算每个事件发生的频率来衡量。这些频率概率可以很好地陈述客观现实。
在现实生活中,很多事情是不能重复的,而且我们获取到的信息往往也是不全面的,往往我们就只能在信息有限的情况下,尽可能做出一个好的预测。贝叶斯框架下的概率理论从另一个角度定义了概率, 他说概率是我们个人的一个主观概念, 表明我们对某个事物是否发生的相信程度。 我们通过观测到的数据对这结果进行更新,从而得到更为准确的估计。相较于上文中已知一个骰子是什么样的情况下去统计或者计算每个点数的情况,更多的时候是我只知道一个骰子抛出了4、6、5的序列,要推测这个骰子是4面、6面、8面、12面还是20面的骰子。这时候贝叶斯概率就该出场了。

贝叶斯公式:
P(A)是A的**先验概率**或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。
P(A|B)是已知B发生后A的条件概率,称作A的**后验概率**。
P(B|A)是已知A发生后B的条件概率,也称之为似然度 。
P(B)是B的先验概率或边缘概率,也作标准化常量(normalized constant)。
如何计算贝叶斯概率
我们现在已经知道了贝叶斯公式,那如何套用公式计算出各种骰子的可能性呢?我们用python来模拟一下贝叶斯分析的过程。
首先我们定义P(A)是骰子为某种类型(4面、6面等)的先验概率。这里我们目前什么都不知道,只知道骰子可能是4面、6面、8面、12面或者20面,那就暂且认为是等概率的好了。
pa = {4: 0.2, 6: 0.2, 8: 0.2, 12: 0.2, 20: 0.2}
接下来解决第二个问题,似然度怎么计算。这个似然度其实就是条件概率,对于M面骰子来说投出1~M的数字D的概率自然是 \frac{1}{M}。这里定义一个函数来表示P(B|A),也就是知道面数后投掷出某个数字的概率:
def likelihood(D, M):
if D <= M:
return 1.0 / M
else:
return 0.0
之后就是第三个问题,P(B)是什么,又如何计算。在这个问题中,A代表骰子为某种类型的先验概率,那B自然代表掷出某一点数的概率。在这里是骰子在不同面数的情况下投掷出某个点数的概率的和。套上公式,定义一个计算函数:
def bayes(prior, likelihood, D):
# 计算每个模型的贝叶斯定理分子。
prob = {M: prior[M] * likelihood(D, M) for M in prior}
# 计算每个模型的贝叶斯定理分母。
norm = sum(prob.values())
# 返回每个模型的后验概率。
return {M: prob[M] / norm for M in prob}
现在,我们知道骰子掷出了一个4,那带入公式计算可得:
p = bayes(pa,likelihood,4)
print(p)
这时计算出来的结果发现掷出一个4的情况下,骰子面数的可能是:
{
4: 0.37037037037037035,
6: 0.24691358024691357,
8: 0.18518518518518517,
12: 0.12345679012345678,
20: 0.07407407407407408
}
代码虽然不长,但是可能不是很直观,所以第一遍计算我们先详细展开一下公式:
首先,在没有其他信息的情况下,预设P(A)是均匀分布的,所以骰子每个面数的概率如下:
其次对于均匀的普通骰子来说,P(B|A)的值也是已知的:
投掷出某个数字的P(B),其实就是各个不同面数的骰子投出某个数字的概率的和:
可以看出求和的部分其实就是原始公式里分子在不同面数情况下的和。所以第一步投出了4,可以算出此时的后验概率P(A|B)为:
手工计算的结果和python代码计算的结果相同。
在进行完一轮计算后,我们发现观察到的投掷骰子的结果,对骰子面数的概率估计产生了影响。我们用已知情况计算出来的后验概率更新一下先验概率P(A),再代入贝叶斯公式不断迭代:
pa = p
p = bayes(pa,likelihood,6)
pa = p
p = bayes(pa,likelihood,5)
print(p)
得到最后的估计:
{
4: 0.0,
6: 0.6353744738305138,
8: 0.26804860614724807,
12: 0.07942180922881423,
20: 0.017155110793423883
}
从观察到的骰子点数序列,反推出有63.54%的概率是6面骰子。这个案例很明显,哪怕稍微对数字有点感觉,你都能一眼看出肯定是6面的概率最高,根本不用计算,但是在复杂情况下,条件、变量一多,直觉肯定是指望不上了。
贝叶斯定理的应用
贝叶斯定理有很多的应用,如果把前文中骰子的例子改造一下,把观测到的点数换成单位时间里战场上新观察到的敌方坦克车身上的编号,如果这个编号也是连续的话,骰子的面数自然就成了敌方兵工厂在单位时间里的产能了。
在真实的二战中,德军正在大规模生产坦克,盟军为了获知其产量使用了多种手段。一方面利用情报人员进行刺探,另一方面根据盟军发现和截获的坦克数量使用统计方法计算。二战之后,盟军对德国的坦克生产记录进行了检查,发现利用统计方法作出的估计令人惊奇地与事实相符1。
| 月份 | 统计估计 | 情报估计 | 德军记录 |
|---|---|---|---|
| 1940.6 | 169 | 1000 | 122 |
| 1941.6 | 244 | 1550 | 271 |
| 1942.8 | 327 | 1550 | 342 |
到了现代社会,贝叶斯定理也有非常多的应用,比如在机器学习上非常经典的贝叶斯分类器,广泛应用于反垃圾邮件。此外还有贝叶斯拼写检查器等。
参考文献
Ruggles, R.; Brodie, H. (1947). "An Empirical Approach to Economic Intelligence in World War II".[J], Journal of the American Statistical Association. 42 (237): 72. ↩